Converting Directional Vectors for an Isometric Field in Unity
In an isometric 2D game, the perspective is tilted to give a sense of depth. This means that moving left or right, or up and down, doesn’t align with the traditional x and y axes in Unity. Instead, we need to adjust our directional input vectors to match the isometric view.

Why Do We Need to Convert Vectors?
When you press the arrow keys or use the joystick in a 2D Unity game, the input is given in standard Cartesian coordinates: x (horizontal) and y (vertical). However, in an isometric game, moving “up” is actually moving diagonally on both the x and y axes. To make our character move correctly on an isometric grid, we need to “rotate” these input vectors to match the isometric angle of our game world.
Getting an Angle Value
Before I can do anything I need to determine the angle at which my horizontal vectors should be tilted. To do this I used a lightweight mac app called “Aequo,” but anything that will let you drop points and get an angle in degrees or radians is good. In Aequo I made two points in a true horizontal line using its angle tool and then a third point along the isometric line on my field and got a value.
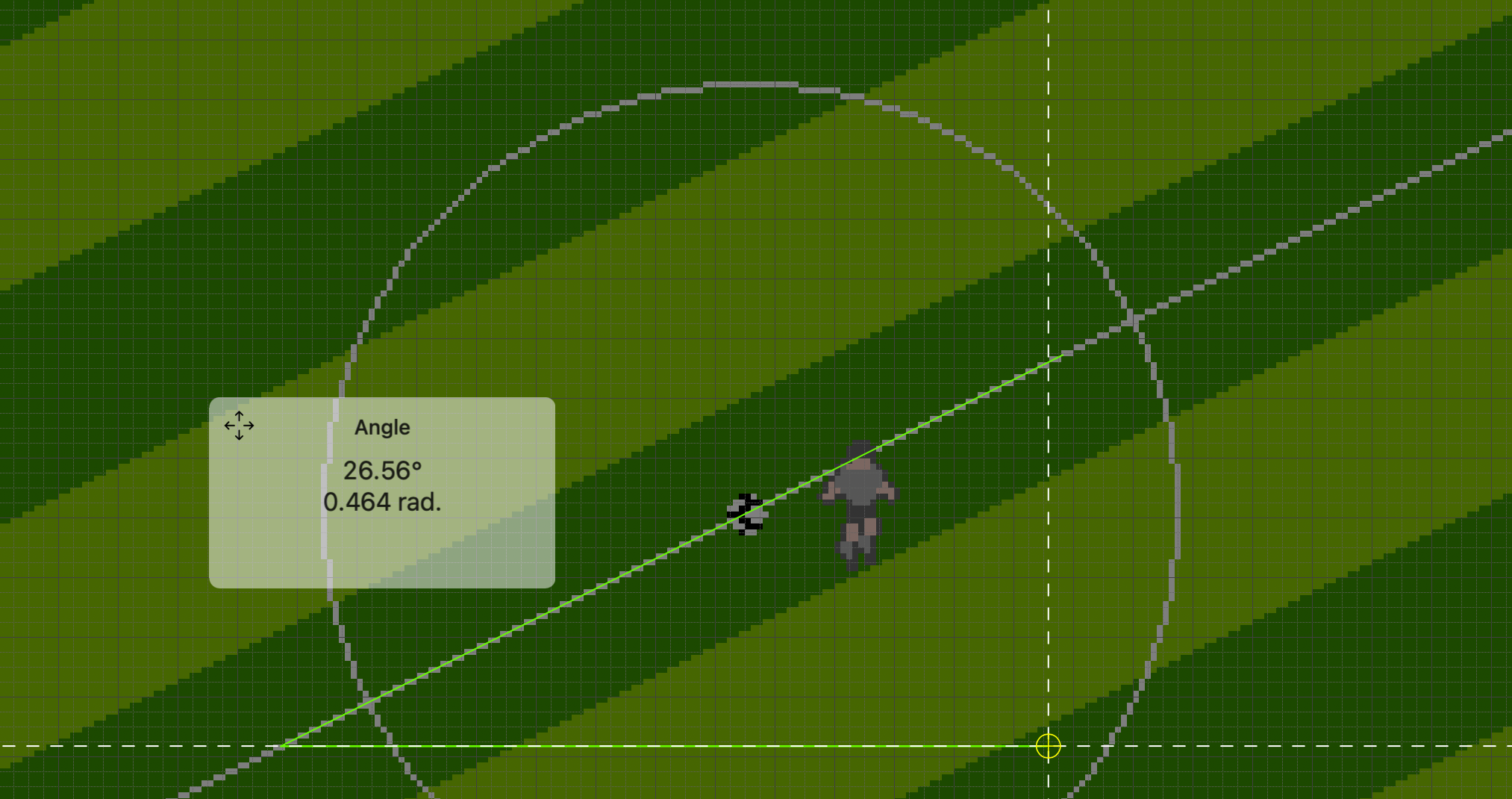
Understanding the Code
In my CharacterController2D script that I’m making for a NES-style soccer game, I’m using the following code snippet to convert the player’s input direction to match the isometric perspective:
private float isoAngle = 26.56f * Mathf.Deg2Rad; // Convert to radians for Mathf functions
//...
float inputX = Input.GetAxisRaw("Horizontal");
float inputY = Input.GetAxisRaw("Vertical");
// Calculate movement direction with isometric adjustment
Vector2 newDirection = new Vector2(
(inputX * Mathf.Cos(isoAngle)) - (inputY * Mathf.Sin(isoAngle)),
(inputX * Mathf.Sin(isoAngle)) + (inputY * Mathf.Cos(isoAngle))
);
Step-by-Step Breakdown
- Reading Input:
inputX and inputY are the raw input values from the player. These values are either -1, 0, or 1, depending on the arrow keys pressed (or joystick movement).
- Define the Isometric Angle:
- We use
isoAngle = 26.56f * Mathf.Deg2Rad to set the angle for the isometric perspective. This angle corresponds to a typical isometric view where the “tilt” is around 26.56 degrees. The tool I used to get the angle actually does a degrees-to-radians conversion on its own, but I am more comfortable working with degrees in general, so I’m letting Unity do that conversion using Mathf.
- Convert Input to Isometric Direction:
-
The new direction vector (newDirection) is calculated by rotating the input vector by isoAngle. This is done using trigonometric functions:
Mathf.Cos(isoAngle) and Mathf.Sin(isoAngle) compute the cosine and sine of the isometric angle.-
The x-component of the new direction is calculated as:
(inputX * Mathf.Cos(isoAngle)) - (inputY * Mathf.Sin(isoAngle))
This effectively rotates the input vector around the origin to align with the isometric grid’s x-axis.
-
Similarly, the y-component of the new direction is calculated as:
(inputX * Mathf.Sin(isoAngle)) + (inputY * Mathf.Cos(isoAngle))
This does the same for the y-axis.
- Normalization:
- After rotating the input, we normalize the vector with
newDirection = newDirection.normalized; to ensure consistent movement speed in all directions.
Why This Works
The above code works because it takes the standard Cartesian input and rotates it by the angle of the isometric grid, effectively “tilting” the controls to match the visual perspective. This allows the player to use simple arrow keys or joystick input while maintaining accurate movement in an isometric world.
For a beginning Unity coder, understanding how to transform vectors like this can be very powerful. It allows for custom controls, camera angles, and even more advanced mechanics like manipulating physics or AI movement in non-standard coordinate systems.
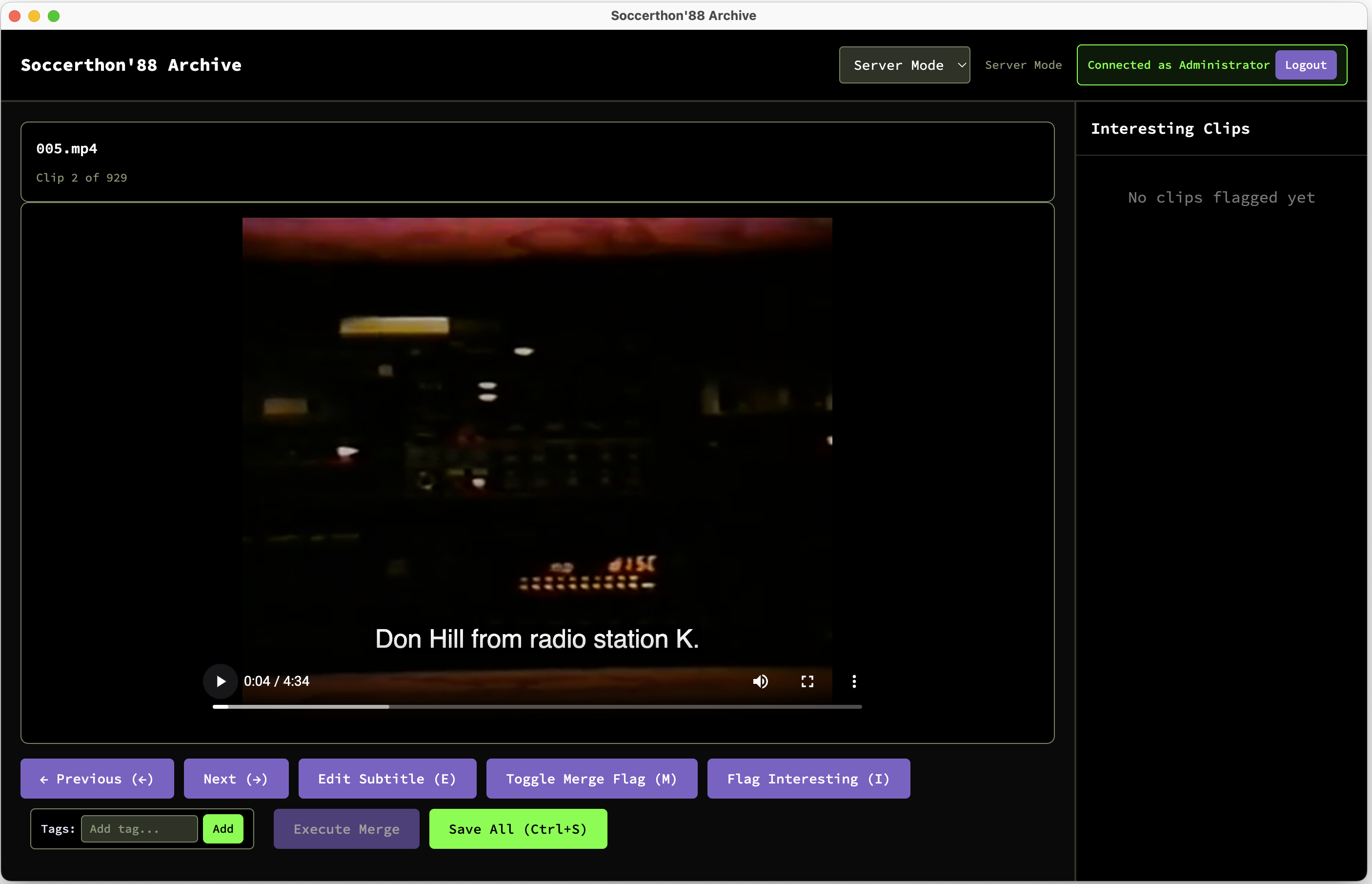 Created an electron app so Danny and I could both tag, merge and edit the subtitles of the clips in the video archive. I feel like engagement with the archive is an activity that will lead to better ideas on how to activate it for players. Some ideas forming between the two of us about game mechanics related to memory, collecting, media, obviously in concert with Danny’s work on The Little Database
Created an electron app so Danny and I could both tag, merge and edit the subtitles of the clips in the video archive. I feel like engagement with the archive is an activity that will lead to better ideas on how to activate it for players. Some ideas forming between the two of us about game mechanics related to memory, collecting, media, obviously in concert with Danny’s work on The Little Database